
회귀 문제
1.일차분석과 시각화
일차 분석
-데이터의 기초통계량을 파악하고 기본적은 그래프로 그려 데이터의 개요를 이해하는 것을 일차분석이라고 한다.
데이터를 처음 받으면 확인해야 할 것
-
결손값
-
특잇값의 유무
-
변수 종류
-
스케일 파악
특징량이 많은 데이터의 경우 pandas의 describe 함수를 이용하여 평균, 표준, 편차, 최솟값, 25,50,74 분위수점등의 기본적인 통계량을 확인한다.
또한, 데이터 내의 수치변수를 히스토그램과 산포도를 통해 확인한다.
2.선형 회귀
선형회귀
-목표 변수와 특징량을 선형함수로 연결한 것
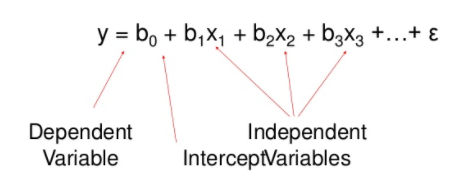
여기서 y는 목표변수, B는 계수, X1는 각 특징량을 나타낸다.
여기서는 미국 주택가격 데이터로 주택가격을 예측하는 선형회귀 분석을 한다.
여기서는 각각의 변수에 대해 주택가격이 얼마만큼의 영향을 끼치는지 확인 할 수 있다. 이 장에서는 수치 변수인 15개의 특징량을 이용하였는데 50프로의 데이터로 학습하고 50프로의 데이터로 시험을 했다.
이때 일반적으로 계수의 유의성은 t 테스트로 불리는 기법으로 검증하였다.
여기서 t값은 독립변수(설명변수)와 종속변수간에 선형관계가 존재하는 정도를 나타낸다. 이
강도가 강할수록 종속변수에 대해 좋은 설명 변수이다.
3.정규화
정규화- 손실함수에 파라미터에 관한 패널티항을 넣는 것
선형회귀 모델을 적용할 때 통계학에서는 공선선에 신경을 써야한다.
공선선-선형회귀에서 특징량간 상관관계가 지나치게 강한 상황
이런모델의 문제는 손실 함수를 최소화하려고 해도 해가 유일하게 정해지지않는다.
-손실함수란 신경망이 학습할 수 있도록 해주는 지표로서 머신러닝 모델의 출력값과 사용자가 원하는 출력값의 차이, 즉 오차를 말한다.
이 문제를 피하기는 방법
-
변수 삭제
-
패널티항을 더하는 방법
이처럼 손실함수에 파라미터에 관한 패널티항을 넣는 것을 정규화라고 한다.
선형회귀의 경우 p = 1 이면 lasso 회귀, p=2 면 Ridge 회귀 라고 한다.
정규화는 공선성 문제와 과적합을 방지하는 효과도 있다.
4.국소선형회귀와 스플라인법
국소선형회귀란?
x축을 몇개의 등간격으로 나누고 몇 개의 선형회귀로 추정하는 방법
즉 유연한 비선형 함수들을 적합하는 기법으로 그 주변의 훈련 관측치들만을 사용하여 적합을 계산하는 것이다.

이렇게 부분으로 나눠서 국소적으로 선형으로 데이터를 만들수 있다.
큐빅 스플라인 - 각 영역에 대해 3차원 다항식으로 피팅 한 것
일반적으로 이런 기법을 회귀 스플라인법이라고 한다.
회귀 스플라인의 경우 경계선(매듭)을 사전에 정할 필요가 있다. 이 경계선을 4분위로 할 수도 있다.
반면 경계선을 자의적으로 정하지 않는 평할 스플라인 기법도 있다.
5.가법모델
가법모델
몇 개의 비모수적인 부분 반응 함수의 합으로 목표 변수를 예측하는 모델

이 가법 모델을 이용하는 이유는 데이터 수가 비교적 적어도 안정되게 추정 할수 있기 때문이다.
즉 선형 모델과 가법 모델의 근사오차의 차가 배리언스의 차를 웃돌지 않는한, 가법 모델을 이용하는 편이 좋다.
가법모델의 특징
-
선형회귀보다 유연하다
-
배리언스가 낮다
-
해석석이 높다
본 내용은 그림으로 배우는 DataScience 데이터 과학을 참고한 내용입니다
'Data scientist > Data Science' 카테고리의 다른 글
| [Data Science] 데이터 사이언스 개념 - 6.분류문제 (0) | 2021.01.14 |
|---|---|
| [Data Science] 데이터 사이언스 개념 - 5.앙상블 학습 (0) | 2021.01.14 |
| [Data Science] 데이터 사이언스 개념 - 3.과적합과 모델 선택 (0) | 2021.01.09 |
| [Data Science] 데이터 사이언스 개념 - 2.머신러닝의 기본 (0) | 2021.01.08 |
| [Data Science] 데이터 사이언스 개념 - 1.데이터 과학이란? (0) | 2021.01.08 |
