반응형
회귀(Regression)
1-1.회귀(Regression)란?
회귀는 독립변수와 한개의 종속 변수간의 상관관계를 모델링 하는 기법으로 보통 머신러닝의 회귀 예측의 핵심은 주어진 피처(속성/독립변수)와 결정 값(종속변수) 데이터 기반에서 학습을 통해 최적의 회귀계수를 찾아내는 것!
간단하게 A(독립변수)와 B(종속변수) 둘의 인과관계나 둘의 연관성? 등을 통해 A라는 속성만 있을 때 B의 값을 예측하는 것이다.
1-2.회귀의 종류
회귀의 종류는 독립변수의 개수에 따라 달라진다.
- 단순선형회귀 - 독립변수 1개
- 다중선형회귀 - 독립변수 2개이상
# 분류와 회귀의 가장 큰 차이는 값의 차이다. 분류는 카테고리값(이산값) 이고 회귀의 결과값은 숫자값(연속값)으로 되어있다.
1-3.구현
# 그래프를 그리는데 필요한 라이브러리
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# 한글 폰트 문제 해결
import platform
from matplotlib import font_manager, rc
# plt.rcParams['axes.unicode_minus'] = False
if platform.system() == 'Darwin':
rc('font', family='AppleGothic')
elif platform.system() == 'Windows':
path = "c:/Windows/Fonts/malgun.ttf"
font_name = font_manager.FontProperties(fname=path).get_name()
rc('font', family=font_name)
else:
print('Unknown system... sorry~~~~')
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
# 키(meter)와 몸무게 (kg)
heights = [[1.6],[1.65],[1.7],[1.77],[1.85]]
weights = [[60],[65],[70],[77],[80]]
plt.title('키&몸무게 그래프')
plt.xlabel('키')
plt.ylabel('몸무게')
plt.plot(heights, weights)
plt.axis([1.5,1.90,55,90]) # 범위
plt.show()

# 회귀나 머신러닝을 할때 sklearn을 사용한다. 여기서는 LinearRegression을 쓴다.
# 라이브러리를 가져오고
from sklearn.linear_model import LinearRegression
# LinearRegression을 쓰기위해 LinearRegression 함수를 Ir_model에 저장한다.
lr_model = LinearRegression()
# fit 함수를 통해 내가 가진 데이터를 모델에 학습한다.
lr_model.fit(heights,weights)
#값을 예측해 본다. predict을 통해 예측을 한다. 여기서는 키가 1.7일때와 1.75일때의 몸무게를 예측한다.
weight_pred = lr_model.predict([[1.7,],[1.75]])
weight_pred
예측 결과 값이 이렇게 두개가 나온다.

# 그래프를 그리는데 여러가지 값을 넣어주고
plt.title('키 & 몸무게 그래프')
plt.xlabel('키')
plt.ylabel('몸무게')
plt.grid(True)
plt.grid(True)
plt.axis([1.5,1.90,55,90])
#선형 회귀 선을 그린다.
plt.plot(heights,weights,'k.')
#여기서는 heights에 대해 예측한 값을 y에 넣고 그래프를 그린다.
plt.plot(heights, lr_model.predict(heights),color='blue')
# 그래프를 그린다.
plt.show()

이렇게 예측에 따른 그래프를 그린다.
예제
## auto-mpg.csv 을 이용한 선형회귀
import pandas as pd
import numpy as np
row_data = pd.read_csv('../data/auto-mpg.csv')
row_data.columns = ['mpg','cylinders','displacement','horsepower','weight','acceleration','model year','origin','name']
row_data.head()

# 데이터의 자료형 확인
row_data.info()

- horsepower 전처리
row_data['horsepower'].replace('?',np.nan,inplace=True)
row_data['horsepower'].unique()
row_data.dropna(subset=['horsepower'],axis=0,inplace=True)
row_data['horsepower'] = row_data['horsepower'].astype('float')
row_data['horsepower'].unique()
row_data.info()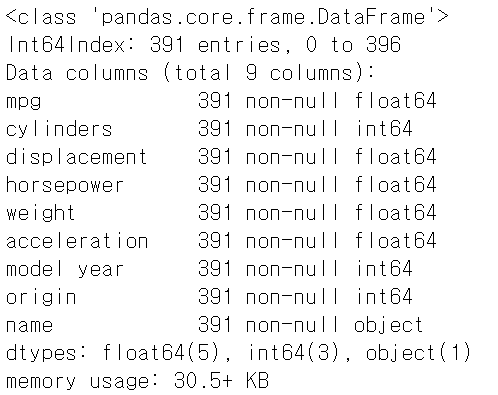
# 분석에 활욜할 독립변수 선택
cor_df = row_data[['mpg','cylinders','horsepower','weight']]
cor_df.head()

# seaborn 산점도
fig = plt.figure(figsize=10,5)
area01 = fig.add_subplot(1,2,1)
area02 = fig.add_subplot(1,2,2)
sns.regplot(x='weight',y='mpg',data=cor_df,ax=area01)
sns.regplot(x='weight',y='mpg',data=cor_df,ax=area02,fit_reg=False)
plt.show()

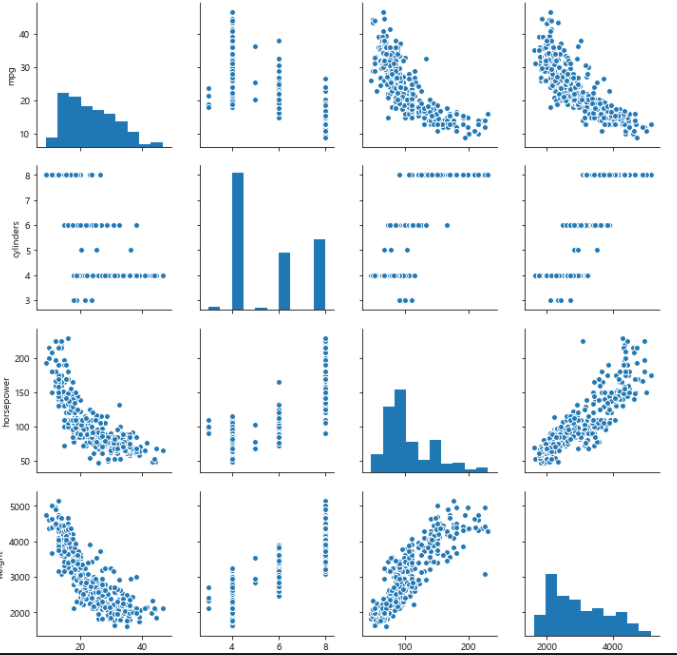
sns.pairplot(cor_df)
plt.show()
# 독립변수
X = cor_df[['weight','horsepower']]
#종속변수
y = cor_df['mpg']
#데이터세트를 구분
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=10)
print(len(X_train))
print(len(X_test))

from sklearn.linear_model import LinearRegression
auto_lr_model = LinearRegression()
auto_lr_model.fit(X_train,y_train)

auto_lr_model.fit(X_train,y_train)
r_square = auto_lr_model.score(X_test,y_test)
print('결정계수 :',r_square)

# 회귀의 기울기
print('기울기:', auto_lr_model.coef_)
# 회귀의 절편
print('절편:', auto_lr_model.intercept_)
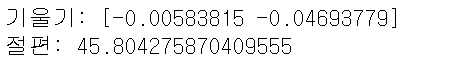
# 모델에 전체 X 데이터를 입력하여 예측값 , 실제값
y_pred = auto_lr_model.predict(X)
y_pred = auto_lr_model.predict(X)
pred_answer = pd.DataFrame(data={'answer ': y, 'prediction' : y_pred })
pred_answer.head()

sns.distplot(y,hist=False,label='answer')
sns.distplot(y_pred,hist=False,label='guess')
plt.show()
이건 예측값과 답에 대한 그래프를 그렸을 때의 결과이다.
반응형
'Data scientist > Machine Learning' 카테고리의 다른 글
| [Dacon] 심리 성향 예측 AI 경진대회 - Auto ML 하는 방법 (2) | 2021.06.21 |
|---|---|
| [ML/DL] 베이지안 최적화(Bayesizan Optimization)란? (0) | 2021.06.09 |
| [ML/DL] 군집화의 정의와 종류 및 구현 (0) | 2021.01.07 |
| [ML/DL] XGboost의 정의와 구현 및 hyper parameter 설정 (0) | 2020.11.13 |
| [ML/DL] 앙상블 학습 (Ensemble Learning): 3.Boosting(부스팅)이란? (0) | 2020.11.05 |
